Le plus petit commun multiple (P.P.C.M) de deux entiers non nuls a et b peut être calculé comme la valeur absolue du produit de a et b divisée par le plus grand commun diviseur (ou P.G.C.D.) de a et b.
En utilisant l'algorithme d'Euclide pour le calcul du PGCD, nous avons l'algorithme suivant :
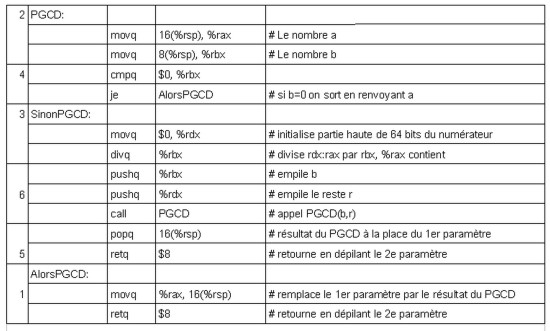
Fonction PGCD(a:nombre, b:nombre):nombre
Si b=0
| alors PGCD=a
Sinon
| r egal au reste de la division (entière) de a par b
| PGCD=PGCD(b, r)
Finsi
et
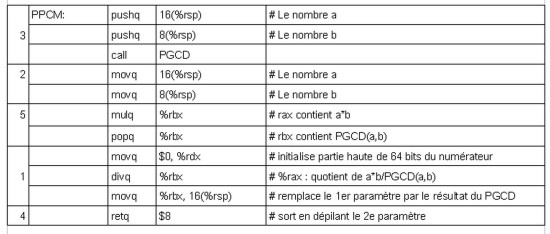
Fonction PPCM(a:nombre, b:nombre):nombre
PPCM=a*b
Si PPCM < 0
| alors PPCM=-PPCM
FinSi
PPCM=PPCM*PGCD(a,b)
Remettez dans l'ordre les lignes des programmes assembleur correspondant à ces 2 fonctions :
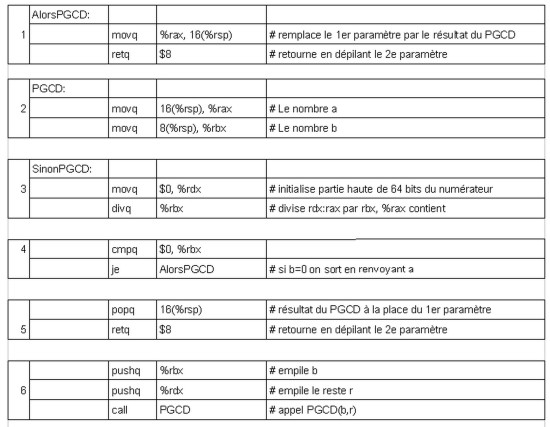

Complétez les cases ci-dessous avec les numéros des blocs de ligne de façon à remettre les programmes présentés ci-dessus dans l'ordre.